Flow Analysis and Resistance Characteristics of Large Butterfly Valves

Abstract: Numerical simulations were conducted to analyze the steady-state flow field of a large-diameter butterfly valve at different opening angles. The flow field characteristics were analyzed for valve openings ranging from 10° to 90°, and the corresponding pressure loss coefficients and flow resistance curves were generated. The results indicate that the flow performance of the butterfly valve decreases significantly at opening angles below 60°. This study provides theoretical guidance for the selection and design of butterfly valve systems. In the central and western regions of China, large- and medium-sized hydropower stations typically use large-diameter butterfly valves or ball valves as the main control valves. A butterfly valve, also referred to as a flap valve, is a regulating valve primarily consisting of a valve body, disc, stem, and sealing assembly. Butterfly valves are characterized by a simple structure, light weight, low material consumption, compact installation dimensions, low actuation torque, and ease of operation. Butterfly valves have a simple structure, are lightweight, consume minimal material, have compact installation dimensions, require low actuation torque, and are easy to operate. Compared with ball valves, butterfly valves also offer advantages in terms of manufacturability and sealing performance. As a result, large-diameter butterfly valves are widely used to regulate the flow of various fluids, including air, water, steam, corrosive media, slurry, oil, liquid metals, and radioactive substances, and are extensively employed in the petroleum, chemical, and power industries.

The flow behavior of the fluid inside a valve has a significant impact on its flow characteristics and operational performance. Numerous researchers, both in China and internationally, have studied valve flow characteristics using a variety of approaches, including theoretical analysis, experimental testing, and numerical simulation. These studies have explored how various valve structures influence the internal flow field and the valve’s flow capacity. Huo Zenghui performed numerical simulations to investigate the internal flow field of a butterfly valve. Using computational fluid dynamics (CFD) and the fundamental governing equations of fluid motion, he analyzed the valve’s internal flow behavior and produced pressure and velocity contour plots for nine different valve openings. Based on these results, he analyzed the flow characteristics at each valve opening and summarized the overall internal flow patterns. By extracting data from the pressure and velocity distributions, empirical formulas were then used to calculate the valve’s flow coefficient and flow resistance coefficient. Huang C.D. and Kim R.H. investigated incompressible flow through a butterfly valve using three-dimensional simulation techniques and generated velocity and stress field contour plots. Ogawa K. and Kimura T. analyzed the torque and flow resistance characteristics of butterfly valves, respectively. Zhang Qinzhao et al. experimentally measured the flow resistance coefficient of a DN680 triple-eccentric butterfly valve at different openings and flow velocities. Numerical analysis showed that, when fully open, the disc of a triple-eccentric butterfly valve produces more vortices than that of a concentric butterfly valve. Consequently, the disc geometry of the triple-eccentric valve can be optimized to reduce the flow resistance coefficient. Yang Yan et al. designed a new eccentric butterfly valve structure and used numerical simulations to analyze its pressure, velocity, and streamline distributions, thereby determining its flow and resistance characteristics. The results indicated that the new design increased the flow resistance coefficient at small openings, reduced the rate of flow change during valve closure, and effectively mitigated water hammer.

GAO Z.X. et al. used the commercial CFD solver Fluent to investigate the effect of structural parameters on the resistance coefficient of butterfly valves. Their findings showed that as the valve opening increases, the flow coefficient rises, while the resistance coefficient decreases. ZHOU X.M. et al. proposed a standard CFD-based calculation method and applied it to calculate the flow coefficients of three butterfly valves, one eccentric rotary valve, and one sleeve valve. The accuracy of this numerical method was validated, with a maximum error of only 2.99%. WU S.X. et al. developed a gas-ring-type pipeline control valve with a lower resistance coefficient, based on the design of a butterfly-type control valve. Through a comparative analysis of the flow field characteristics of the two designs, they found that the proposed valve exhibited lower wall shear stress and a reduced maximum flow velocity. YANG Jiaming et al. used numerical simulations to determine the flow characteristic curve and flow field distribution of a pressure regulator spray valve. They compared the simulation results with actual operating conditions, thereby confirming the accuracy of the numerical method. QIAN Jinyuan et al. conducted numerical simulations of porous plates to analyze their flow characteristics and investigated the relationship between pressure drop and internal flow behavior based on their geometric parameters. To address flow disturbances in butterfly valves, YU Jianping et al. reviewed and summarized studies on the hydrodynamic torque characteristics of butterfly valves in China and internationally, comparing their applicability and accuracy to provide theoretical guidance for butterfly valve design in China. Therefore, analyzing the internal flow behavior of fluid within a butterfly valve is essential for understanding its flow characteristics. In this study, the authors employed the numerical simulation software Fluent to investigate the flow characteristics and flow resistance of large-diameter butterfly valves at various openings, providing valuable insights for valve design and optimization.

The solid model and internal schematic of the large-diameter butterfly valve are shown in Figures 1 and 2. The valve primarily consists of a body, stem, disc, and sealing assembly. The butterfly valve has an inner diameter of 4800 mm. As the stem rotates, the valve opening gradually increases from 0° to 90°.

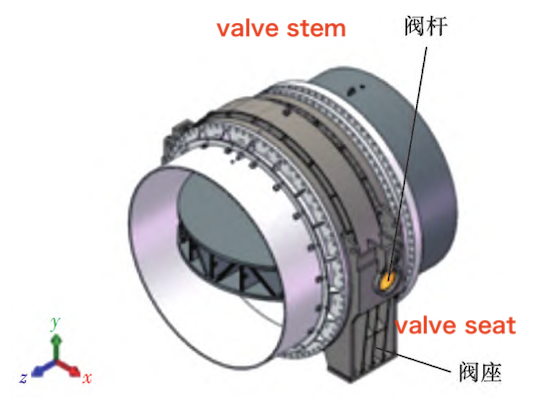
Figure 1. Structure of a Large-Diameter Butterfly Valve

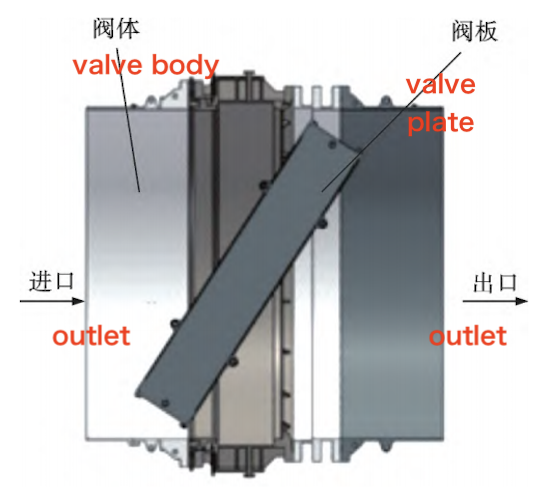
Figure 2. Internal Schematic of a Butterfly Valve

To simplify meshing and improve mesh quality, the geometry of the butterfly valve was appropriately simplified. Features that did not affect the flow characteristics were removed, and the valve flow passage was extracted. Due to the structural symmetry of the model, only half of the flow domain was used in the simulation to reduce computational complexity. The inlet and outlet pipes were extended to lengths of five and ten times the valve’s inner diameter, respectively, to ensure fully developed flow conditions.

The computational domain was meshed using the pre-processing software Mesh in ANSYS Workbench. To balance computational efficiency and accuracy, a hybrid mesh was employed to discretize the flow channel model. After several iterations, it was found that when the total number of mesh elements reached approximately 600, 000, the outlet mass flow rate no longer changed significantly with further mesh refinement (Table 1). Accordingly, the mesh sizes were set as follows: 100 mm for the inlet and outlet extension pipes, 20 mm for the flow passage between the valve discs, and 60 mm for the remaining regions. As shown in Figure 3, the final model contained 6, 248, 368 elements.

Figure 3 The flow channel grid model of large-diameter butterfly valves

Table 1 Verification of Grid Independence

The DN4800 hydraulically controlled butterfly valve regulates parameters such as water pressure and flow rate by adjusting the opening and closing of the valve disc. In this study, numerical simulations were conducted for various valve openings to analyze water flow through the DN4800 valve. The flow resistance coefficients at different opening angles were calculated. The operating conditions were set as follows:

Nominal pressure: PN 10

Opening angle: 10°–90°

Inlet velocity: 3 m/s

Outlet pressure: 0 MPa

Analysis of the operating conditions indicates that the DN4800 valve has a large orifice diameter and high inlet and outlet velocities, leading to turbulent flow. Furthermore, the throttling effect of the valve disc intensifies turbulence within the flow field. Therefore, a turbulence model is necessary for the numerical simulation. Assuming the working medium is liquid water at room temperature, the fluid properties were defined accordingly. When the Reynolds number exceeds a critical value, the flow transitions from laminar to turbulent. A pressure-based solver was employed, using the standard k–ε turbulence model and the SIMPLE algorithm for pressure–velocity coupling. All solid boundaries were defined as no-slip walls. The inlet was assigned a velocity-inlet boundary condition, and the outlet was defined as a pressure-outlet boundary with an operating pressure of 0 MPa. The calculated turbulence intensity was 2.04%.

The flow resistance coefficient represents the flow capacity of the butterfly valve. According to the Valve Design Manual, the coefficient for turbulent flow can be calculated using the following formula:

where:
Δp — pressure differential across the butterfly valve (Pa);
v— mean fluid velocity through the valve (m/s);
ρ — fluid density (kg/m³);
ξ — flow resistance coefficient of the butterfly valve.

Numerical simulations were conducted to analyze the internal flow characteristics of a DN4800 butterfly valve at various openings, with an inlet velocity of 3 m/s and atmospheric pressure at the outlet. Due to the obstruction caused by the valve disc, the fluid experiences significant disturbances, resulting in unsteady flow patterns. Therefore, analyzing the velocity and pressure distributions at different openings is essential for evaluating the valve’s flow capacity.

The stability of the velocity field in a butterfly valve determines the smoothness of fluid flow, and variations in velocity are a key indicator of flow behavior. Figure 4 shows the velocity contours along the symmetrical plane of the butterfly valve for opening angles ranging from 10° to 90°. At a 10° opening, the flow passage is extremely restricted, causing severe throttling and strong flow contraction. The maximum velocity reaches 98.6 m/s, leading to pronounced backflow and vortex formation. When the opening increases to 30°, the vortex region expands and gradually shifts downstream from the disc center toward the pipe wall. As the opening continues to increase, the upstream flow velocity decreases, flow nonuniformity is reduced, and the downstream vortices weaken, resulting in a smoother flow. At a 70° opening, most vortices disappear, although minor flow disturbances persist. When the disc is fully open (90°), the velocity distribution becomes uniform across the entire flow field, with no significant vortices and a stable flow pattern. As shown in Figure 4, two high-speed jet zones form downstream of the valve disc—one at the upper edge and one at the lower edge. The areas of these zones initially increase and then decrease as the valve opening expands. When the valve opening is small, the maximum velocity is high, but the jet zones remain limited in size due to the restricted flow area. As the opening increases, the disc’s obstruction weakens, the flow area expands, and the jet zones enlarge. As the opening continues to increase, the enlarged flow passage reduces the throttling effect, thereby decreasing the maximum velocity and contracting the jet zones.

Figure 5 illustrates the variation of maximum velocity with valve opening. The maximum velocity within the flow field decreases as the valve disc opening increases. For openings below 40°, the maximum velocity decreases sharply as the valve opens. Between 50° and 80°, the maximum velocity continues to decline, but at a slower rate, eventually approaching a stable value. At a 90° opening, the maximum velocity reaches 4.5 m/s, approaching the inlet and outlet velocities, which indicates that the disc’s throttling effect has been significantly reduced.

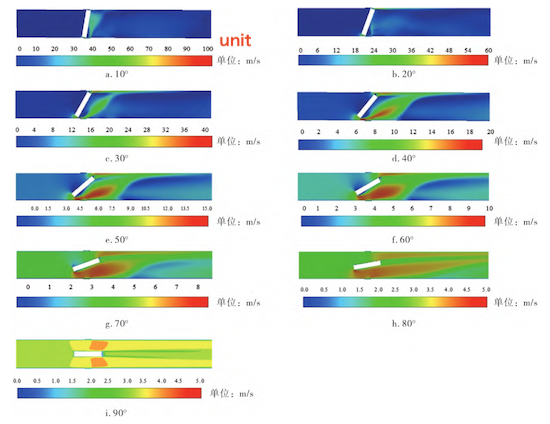
Figure 4 The velocity distribution of the symmetry plane under different openings

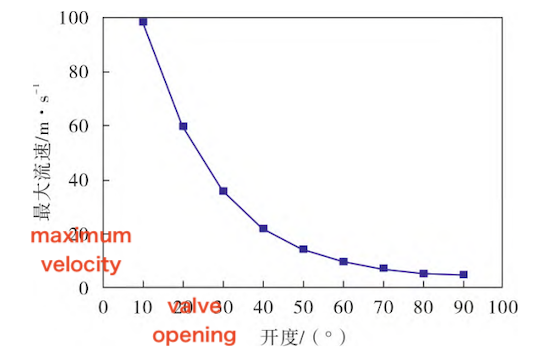
Figure 5 Variation of Maximum Velocity on the Symmetrical Plane with Valve Opening

Pressure variation within a butterfly valve at different openings is crucial for assessing its flow capacity, structural integrity, and hydrodynamic torque. Therefore, analyzing the pressure distribution is essential for understanding the overall flow behavior. The pressure contours for various openings are shown in Figure 6.

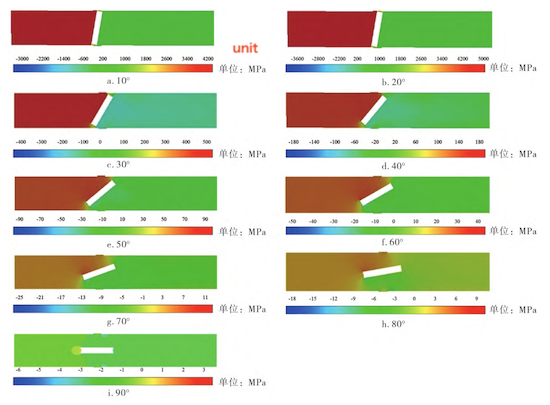
Figure 6 Pressure Distribution Contours on the Symmetrical Plane at Different Openings

As shown in Figure 6, both the maximum pressure and the overall pressure differential within the flow field decrease as the valve opening increases. At a 10° opening, the pressure across the disc varies sharply, creating a large low-pressure zone between the disc and the valve body. The minimum pressure occurs near the center of the disc, where vortices are generated. As the opening increases, pressure nonuniformity within the flow field gradually diminishes. At a 60° opening, localized low-pressure regions persist near the disc. When the opening reaches 80°, minor pressure differences remain due to fluid turbulence, but the overall pressure distribution becomes more uniform. At a fully open (90°) position, the fluid velocity near the disc drops sharply upon impact, generating small, localized high-pressure fluctuations. The overall pressure differential across the disc is nearly zero, and the pressure distribution remains essentially stable, although a slight pressure drop still occurs due to the presence of the disc. A distinct low-pressure region is observed along the edge of the disc for openings between 0° and 60°. The saturated vapor pressure of water at 25 °C is 3.169 kPa (absolute pressure). Within this range, the local pressure drops below the saturated vapor pressure, potentially causing cavitation that can erode the valve disc and reduce the service life of the butterfly valve. In practical applications, butterfly valves should be operated within appropriate opening angles and working conditions to prevent cavitation. Regular inspections and maintenance are recommended to ensure long-term safe operation.

The flow resistance coefficient is an inherent property of a butterfly valve and serves as a key parameter for assessing its hydraulic performance. However, the flow resistance characteristics of butterfly valves are complex, depending on factors such as valve geometry, disc position, and flow conditions. To evaluate the flow capacity of the butterfly valve, the pressure differential between its upstream and downstream sides was determined, and the corresponding flow resistance coefficient was analyzed using numerical simulation. Based on the simulated internal flow fields at different valve openings, the pressure differential across the valve disc at each opening was calculated. The flow resistance coefficients for butterfly valves with different disc thicknesses were then calculated using the standard formula. To determine the pressure differential (Δp) across the valve, the difference between the inlet and outlet pressures of the flow channel model was measured, and the pipeline resistance loss was subtracted to obtain the pressure drop attributable solely to the valve. Using these calculated pressure differentials, the flow resistance coefficient was determined for each valve opening and disc thickness according to the standard flow resistance formula. These results provide a quantitative basis for analyzing the effects of structural parameters and valve opening angles on the hydraulic performance of large-diameter butterfly valves.

Based on the measured pressure differentials and calculated flow resistance coefficients at various openings, a curve illustrating the variation of the butterfly valve’s flow resistance coefficient with valve opening was plotted (Figure 7). As the valve opening increases, the flow resistance coefficient gradually decreases. When the opening is below 30°, the coefficient declines sharply with increasing valve opening. Between 30° and 50°, the rate of decrease slows, and when the opening exceeds 60°, the flow resistance coefficient stabilizes. In this case, the initial thickness of the butterfly plate truss is 60 mm.

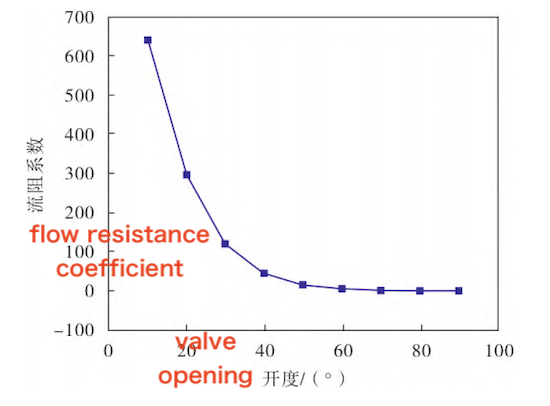
Figure 7 Variation of Flow Resistance Coefficient with Valve Opening

A comparative analysis of flow resistance was performed for butterfly valves with different truss thicknesses. Table 2 shows the variation of the flow resistance coefficient with valve opening for truss thicknesses of 40 mm and 60 mm. At small valve openings, truss thickness has a significant effect on the flow resistance coefficient. The valve with a 60 mm truss thickness shows a considerably higher flow resistance coefficient than the 40 mm valve, and the coefficient decreases sharply as the valve opens. When the valve opening exceeds 40°, the flow area expands, and the flow resistance coefficient gradually stabilizes. At this stage, truss thickness becomes a secondary factor affecting flow performance, and the coefficients for different truss thicknesses tend to converge.

Table 2. Variation of Flow Resistance Coefficient with Truss Thickness

As the butterfly valve opening increases, the maximum flow velocity gradually decreases, and the flow becomes smoother. When the opening is below 40°, pronounced vortices form downstream of the disc, highlighting areas where structural optimization could improve flow capacity. The flow resistance coefficient decreases as the valve opening increases. When the opening is below 50°, the coefficient drops sharply. Beyond 50°, it gradually stabilizes. A significant difference in flow resistance is observed between small and large openings. Simulation results indicate that decreasing the disc thickness increases the effective flow area, reduces pressure loss, and enhances the flow capacity. However, when the disc opening is between 40° and 60°, strong vortices form downstream, potentially causing erosion and damage to the disc. Therefore, further structural optimization is recommended to minimize flow resistance and improve the overall hydraulic performance of the butterfly valve.